The Seventh SoMaS Team Mathematics Challenge

The proud country of Whereveria has been run by the Fair party for many years. All its 1000 citizens have an income of one florin per day. However, one day the Greedy party, led by the self-serving Mr Wrongson, gets elected. Mr Wrongson announces that he will hold a series of referenda. Each referendum proposes new incomes for everyone, which must be integer numbers of florins per day, adding up to 1000. Mr Wrongson always votes for his own proposal. Other people will vote for a proposal if it makes them richer, against if it makes them poorer, and not vote at all if it doesn't change their income. Proposals pass if there are more votes for than against. What's the highest income that Mr Wrongson can end up with?

Inhabitants of a far-away planet called Tpyge only have unit fractions such as \(1/2, 1/3, 1/4, \dots\) and express all other fractions as finite sums \begin{equation}\label{eq:frac} \frac1{a_1} + \frac1{a_2} + \dots + \frac1{a_r} \end{equation} where all \(a_i\) are distinct natural numbers. For example, instead of \(\frac23\) they write \(\frac12 + \frac16\) (note that \(\frac13 + \frac13\) is prohibited).

1. Prove that any rational number \(\alpha\in(0,1]\) can be expressed as a Tpygian fraction in infinitely many distinct ways.
2. What is the shortest Tpygian expression for \(\frac2n\) and \(\frac3{n}\), and do you have any comments or generalizations?

Can you tile a square with a finite number of non-convex quadrilaterals?

What is the optimal strategy for updating a lego calendar from one month to the next? i.e. the minimal number of separations and glues. The thin red lines are made from pieces 4 units long.

Following a coup d'état, Mr. Wrongson from Question 1 goes on the run and builds himself a house in the wilderness as shown below.



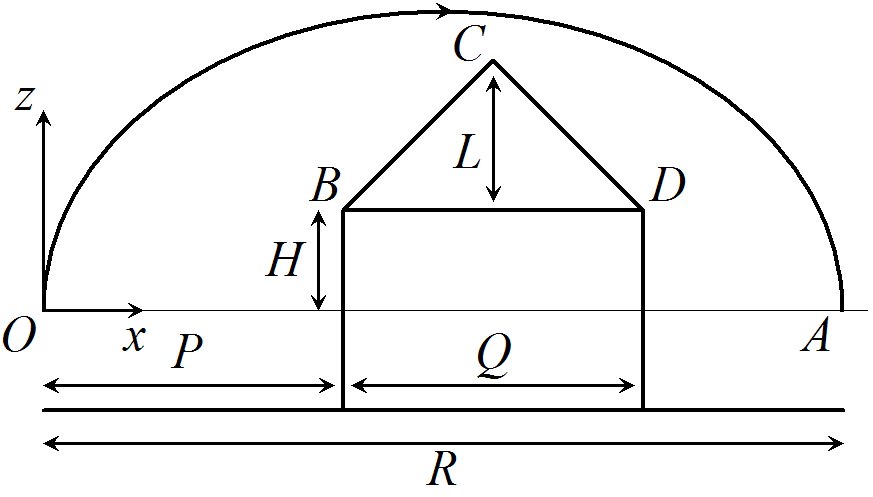
Wrongson is bored and wonders whether he can throw his purse over the roof of his house, run through the house and catch the purse on the other side before it bounces. The following challenge is to use a mathematical model to assess whether this feat is actually possible.

Assume that the purse is thrown with speed a \(V\) and that Wrongson can run straight through his house without hindrance. The purse is projected from the origin \(O\) with speed \(V\) at an angle \(\theta\) to the horizontal and Wrongson hopes to catch the purse at the point \(A\) which is on the same horizontal level as \(O\). Define distances \(P\) and \(Q\) as the distance from \(O\) to the first side of the house and the distance from one side of the house to the other, as shown in the diagram. Define \(H\) as the height of the bottom of the roof above \(O\), and \(L\) as the height of the apex of the roof above the bottom of the roof as shown. The distance \(R\) is defined to be the total horizontal distance travelled by the purse. Ignore air resistance and the spin of the purse. Wrongson's house has \(H=5\) m, \(L=2\) m, \(Q=10\) m. Suppose that \(P=10\) m and that the initial speed of projection \(V\) is 20 m s\({}^{-1}\). Take the acceleration due to gravity to be \(g=9.8\) m s\({}^{-2}\).

1. Find all possible angles of projection for the ball to clear the house.
2. Calculate the minimum average running speed of Wrongson in order for him to be able to catch the ball.
3. Discuss whether you think, with these values of \(H\), \(L\), \(P\), \(Q\), and \(V\), that Wrongson could have realistically performed this feat.
4. The size of the house is fixed. What effect will changing \(V\) or \(P\) have on the angle of projection and the average running speed required if Wrongson is to achieve this feat?
5. Discuss whether you think Wrongson could achieve this feat, the validity of the model used, and other factors which could be incorporated into the model.