Question 3
A cloning move on an object at the point \( (n,m) \) moves the object to the point \( (n,m+1)\) and puts a clone on \( (n+1,m) \). Cloning moves are permitted only if \( (n,m+1) \) and \( (n+1,m)\) are unoccupied. If Dolly the sheep is standing at the origin and all other points are unoccupied, can she find a sequence of cloning moves that allow Dolly and her clones to escape from the set \( \{(0,0), (1,0), (0,1), (2,0),(1,1),(0,2)\}? \)
Solution by Elastic Pancakes
We begin by defining an invariant on the placement of Dolly and her clones. Note that we can represent each point by a square for easier visualisation, so that the bottom left square represents \((0,0)\) etc.. Number the squares of the board, as shown below.
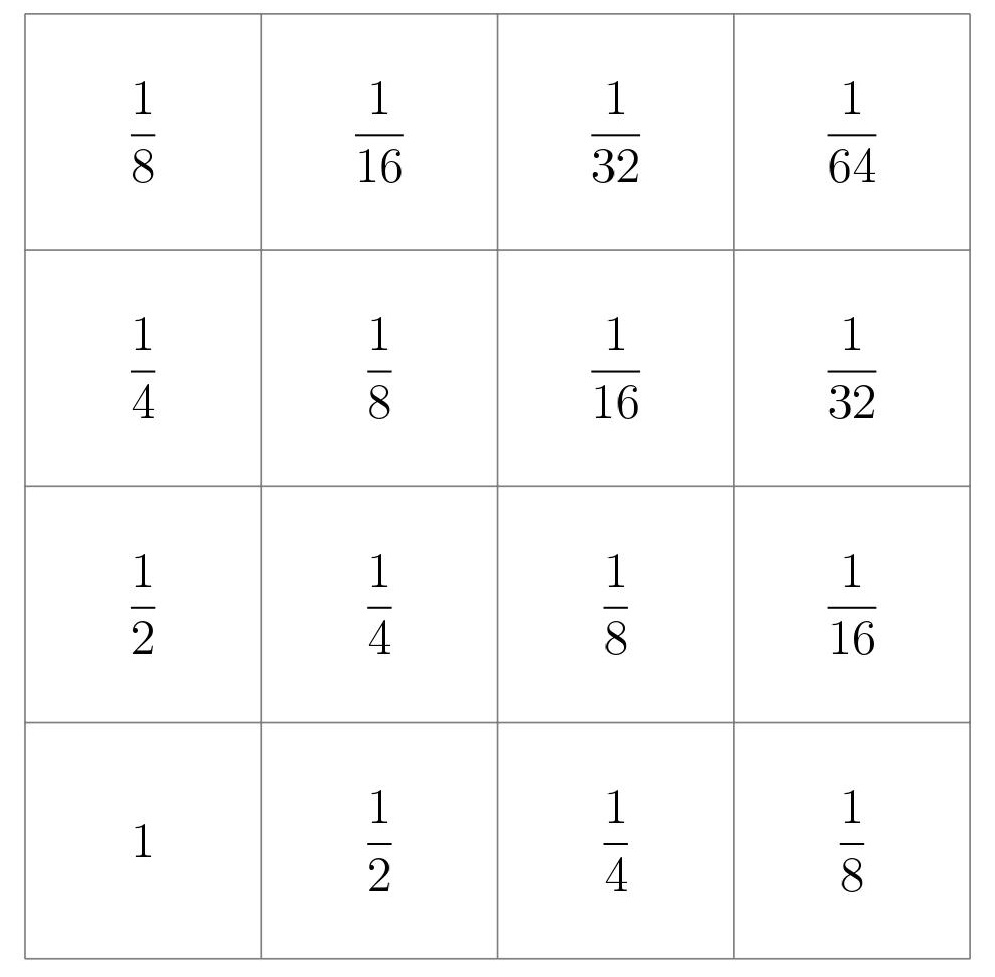
The weight at the beginning, when we just have Dolly, is one. So, throughout the whole game we will always have a weight of one with all our clones. The weight of the bottom row is given by the geometric series \[1+\frac{1}{2}+\frac{1}{4}+... = \frac{1}{1-\frac{1}{2}}=2.\] From this we can calculate the total weight of the board, since (beginning at the bottom row), the weights of the rows are \(2,1,\frac{1}{2},\frac{1}{4},...\). Therefore the weight of whole board is four.
The weight of the set that Dolly and her clones are trying to escape from is \(2\frac{3}{4}\). So the weight outside the set is \(1\frac{1}{4}\). However, we always have exactly one clone in the bottom row. If Dolly and her clones escape then the largest weight we can get from the first row and the leftmost column is \(\frac18\), and similarly for the leftmost column. So, the weight of squares not occupied in the first row/leftmost column is at least \(\frac18\).
We can now see that the weight of the squares occupied outside the set is at most \(1\frac{1}{4}-\frac{1}{8}-\frac{1}{8}=1\). So, in order for Dolly and her clones to escape, we would have to have a clone on every square outside the set union the bottom row and leftmost column, which requires an infinite sequence of moves. Hence it is not possible for Dolly and her clones to escape from the set.