Question 5
Define an \(n\)–colouring of the plane to be a function \[f : \mathbb{R}^2 \rightarrow \left\{c_1, \ldots, c_n\right\}.\] In other words, each point in the plane is coloured one of n colours. For which \(n \in \mathbb{N}\) does there exist an \(n\)–colouring of the plane with the property that no two points in \(\mathbb{R}^2\) at distance 1 apart have the same colour?
Solution by Chums
Firstly, if we can produce an \(n\)-colouring of the plane with this property, we can produce an \((n+1)\)-colouring the same way, by excluding the \((n+1)\)-st colour.
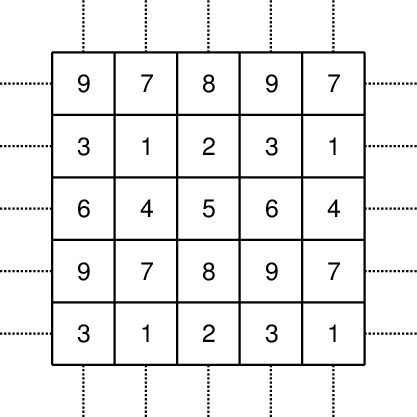
We will consider polygons circumscribed inside circles of diameter slightly less than 1 (say \(0.9\)). This means that any two points inside the polygons will be at most \(0.9\) from each other, and so we can safely colour them one colour.
The following tiling of squares proves we can do it with 9 colours:
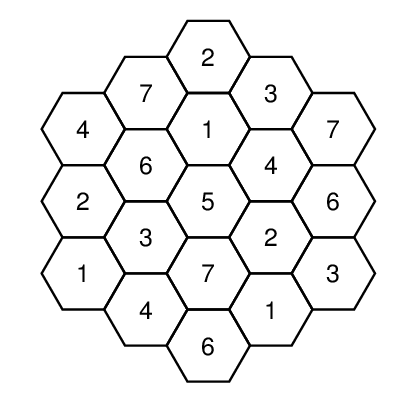
The following tiling of hexagons gets the number down to 7:
Working from the other end to rule out low numbers, one colour is not enough (consider two points distance 1 apart). Two colours are also not enough: consider an equilateral triangle, where no two vertices can be coloured the same.
Three colours are also not enough: it is easy to check that the following arrangement of ten points requires four colours.
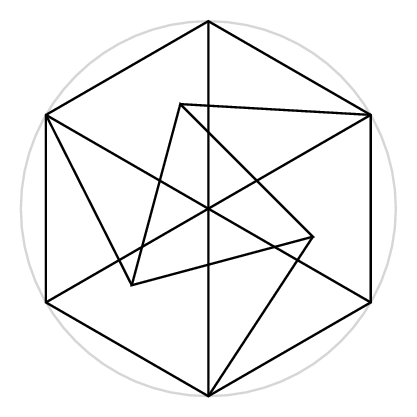
Hence it is possible for seven, but not possible for three.