Question 4

Solution by \(\pi\eta\)

Note, I will be using standard pi day notation: the terms "pie" when referring to the big square, "portions" when referring to the smaller rectangles contained within the pie, and "slice" or "cut" when referring to the lines dividing the pie into portions. We are aiming for everyone to have a square portion of the pie.

Furthermore I am taking \(\mathbb{N}=\lbrace 1,2,3,\ldots\rbrace\), i.e. not including 0.

Firstly, noting that all internal angles of a square are right, it is safe to assume that all cuts must be made parallel to the edges of the pie.

Case of \(n = 1\)

Here is the pie:

Thus the pie can be divided into one square portion (Although the question strictly asks for smaller squares, so this doesn't count).

Case of \(n = 2\)

The only way to divide the pie into precisely 2 portions is to cut exactly once. Without loss of generality, assume the cut is made horizontally, at height \(a\), say:

So we have two rectangular portions. But the only way for the lower \(x\times a\) portion to be \emph{square} is if \(x=a\). If \(x=a\), however, then the upper \((x-a)\times a\) portion will disappear. Thus there is no way to slice a square pie into two square portions.

Cases of \(n = 3, 4\)

The next logical step would be to cut the pie twice. It follows from the previous case that cutting the pie twice horizontally will not yield square portions, as the widths of the portions will remain \(x\), with their heights being diminished with each cut made. Thus the cuts must be made perpendicular to each other. If the cuts bisect the sides of the pie, we obtain 4 square portions:

There will always be 4 portions if we cut in this way, and always 4 or more if we make more than 2 cuts, and as we have shown there is no way of obtaining 3 square portions by either cutting once or twice horizontally, it is safe to conclude that it is impossible to obtain precisely 3 square portions.

Case of \(n\) even

For even \(n\), with \(n>4\), we can show that the pie can be cut into \(n\) portions using the following algorithm. Firstly, the case where \(n=6\). We cut twice, once horizontally and once vertically, at a distance of \(\frac{2x}{3}\) from the edges of the pie:

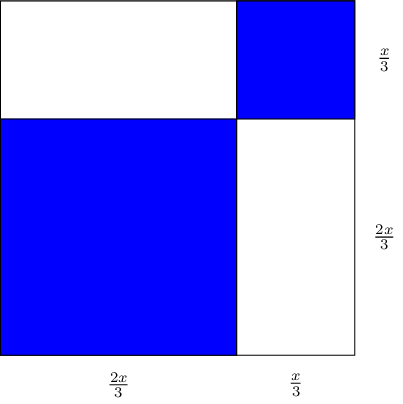
Thus we have two square portions (blue), of size \(\frac{2x}{3}\times\frac{2x}{3}\) and \(\frac{x}{3}\times\frac{x}{3}\). What remain are two congruent regions of size \(\frac{2x}{3}\times\frac{x}{3}\), which we can bisect in order to obtain 4 extra square portions, giving a total of 6:

In general, for \(m\in\mathbb{N}\), by making two cuts at distance \(\frac{(m-1)x}{m}\) from the edges of the pie, we obtain two square portions (blue), and two congruent rectangular portions of size \(\frac{x}{m}\times\frac{(m-1)x}{m}\), which can clearly be divided into \(m-1\) squares of size \(\frac{x}{m}\):

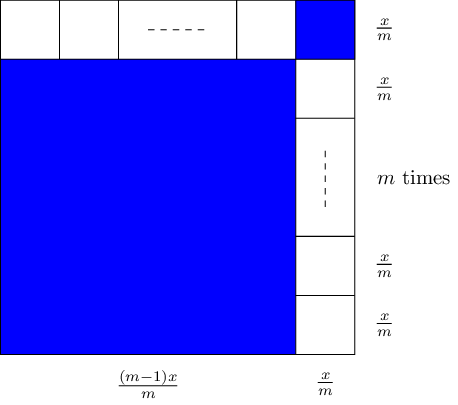
Thus we can obtain \(2m+2\) square portions of pie for all \(m\in\mathbb{N}\).

Case of \(n\) odd

Using the previous two cases, we can show that the pie can be cut into \(n\) portions for odd \(n\), where \(n>5\). By cutting the large \(\frac{(m-1)x}{m}\) portion into 4 equal square portions (as in the case where \(n=4\)), we can obtain \(2m+5\) square portions of pie for any \(m\in\mathbb{N}\):

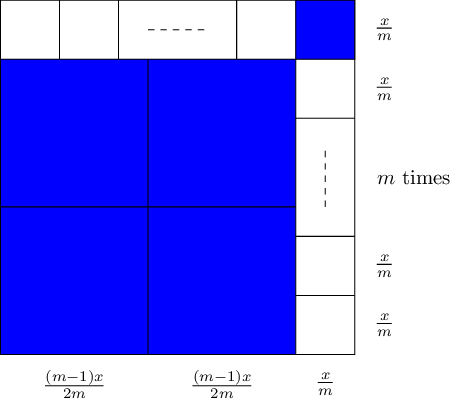
Thus we can obtain \(2m+5\) square portions of pie for any \(m\in\mathbb{N}\).

Case of \(n = 5\)

We have shown thus far that we can obtain \(n\) slices for any \(n=2m+2\) or \(n=2m+5\), \(m\in\mathbb{N}\), i.e. all natural numbers strictly greater than 5, and \(n=4\).

By dividing the pie only into square portions, it has been clear that each vertex of the pie is also the vertex of a square. Thus, we can start by serving up four square portions:

There are two cases for the location of the fifth slice of pie: with one edge against the edge of the pie tin, or without. For the first case, we say, wlog, that the shared edge of the fifth slice and the pie tin is the top edge:

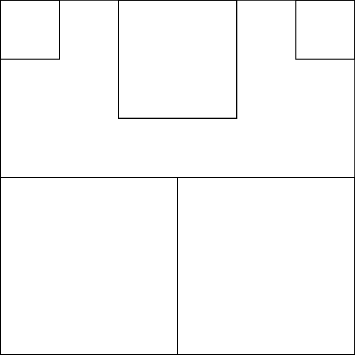
It is clear, now, that the bottom two slices must share a common edge in order to fill the tin, but this either leaves a rectangle of dimensions \(x\times \frac{x}{2}\), which cannot be cut into three square portions, or a figure as below:

Where, again, the white region, no matter the dimensions of the portions already served, cannot be filled by a single square.

Similarly, it can be seen that if the fifth portion does not share an edge with the side of the tin, the edges of the tin must be lined by the remaining four slices. It can be shown by evaluating the area and the perimeter of the pie that, with \(x\) the width of the pie, \(x_i\) the widths of the four served slices, and \(s\) the width of the fifth slice, \[x_1^2+x_2^2+x_3^2+x_4^2+s^2=x^2,\] \[x_1+x_2=x_2+x_3=x_3+x_4=x_4+x_1=x.\] Substituting the latter equations into the former gives \[x_1^2+(x-x_1)^2+x_1^2+(x-x_1)^2+s^2=x^2,\] And thus \[x^2-4xx_1+4x_1^2+s^2=0,\] or, factorising, \[(x^2-2x_1)^2+s^2=0.\] This has the unique solution \(x_1=x/2\), \(s=0\), demonstrating that there cannot be a way of slicing the pie into five portions.

We have shown, thus, that a pie can be sliced into \(n\) strictly smaller square portions for any \(n\in\mathbb{N}\setminus\lbrace 1,2,3,5\rbrace\).