Question 3

Official Solution by Fionntan Roukema

Existence

Let \(T\) be an acute angled triangle with side lengths \(a,b,c\). We suppose with out loss of generality that \(a\leq b\leq c\). We consider the cuboid \(C\) with side lengths equal to \(x,y,z\) where \[ x=\sqrt{\frac{a^2+b^2-c^2}2},\qquad y=\sqrt{\frac{a^2+c^2-b^2}2}, \qquad z=\sqrt{\frac{c^2+b^2-a^2}2}. \] As \(a\leq b\leq c\) we can see that the cube is non-degenerate provided that \(a^2+b^2-c^2>0\). The law of cosines guarantees that this is the case when the angle opposite the side with length \(c\) is acute. Using Pythagoras's Theorem we can see that the diagonals of the cuboid have lengths \(a\), \(b\), and \(c\) (see the diagram below).

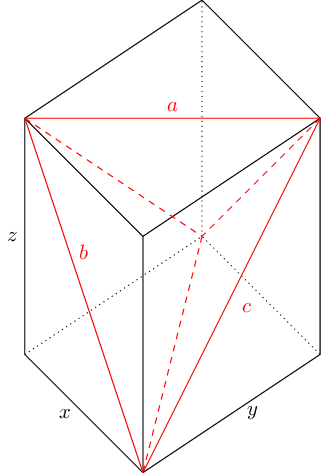
The convex hull of the highlighted diagonals in the cuboid above is a tetrahedron \(\Delta\) whose faces consist of four congruent triangles with side lengths \(a\), \(b\), \(c\). A triangle is uniquely determine by three edge lengths. Therefore, the tetrahedron \(\Delta\) has four faces congruent to \(T\).

Uniqueness

We will now show that if there exists a tetrahedron \(\Delta\) in \(\mathbb{R}^3\) whose faces are congruent to \(T\) then it is unique. We may assume that three of the vertices have coordinates \(v_1=(0,0,0)\), \(v_2=(c,0,0)\) and \(v_3=(\alpha,\beta,0)\) where the distance from \(v_1\) to \(v_3\) is \(b\) and the distance between \(v_2\) and \(v_3\) is \(a\).

As each vertex is connected to three edges of lengths \(a,b,c\), any point \(v_4=(x,y,z)\) in \(\mathbb{R}^3\) that is the fourth vertex of a tetrahedron whose faces are congruent to \(T\) satisfies: \[x^2+y^2+z^2=a^2\] \[(x-c)^2+y^2+z^2=b^2\] \[(x-\alpha)^2+(y-\beta)^2+z^2=c^2\] Note that the first two equations determine \(x\) uniquely. The value of \(x\) in the second two equations determines \(y\) uniquely.

Substituting the values of \(x\) and \(y\) into (1) determines \(z\) up to sign. The two constructed tetrahedra are congruent via a reflection in the \(xy\)-plane.

Volume

We now calculate the volume of \(\Delta\). The cuboid \(C\) consists of the tetrahedron \(\Delta\), and four corners each of which has volume \(\frac{xyz}6\) (as it is well-known that the volume of a cone with height \(h\) over a domain \(D\) is \(\frac{h}3\textrm{area}(D)\)). Thus \[ \text{vol}(C)=\textrm{vol}(\Delta)+4\left(\frac{xyz}6\right)\qquad\text{and so}\qquad \textrm{vol}(\Delta)=\frac{xyz}3. \] Substituting back in the values we know, we get, \[ \textrm{vol}(T)=\sqrt{\frac{(a^2+b^2-c^2)(a^2+c^2-b^2)(b^2+c^2-a^2)}{72}}. \]