Question 2
The following picture shows a (not to scale) triangle which is divided into four regions. The areas of three of the regions are shown. Find the area of the shaded region.
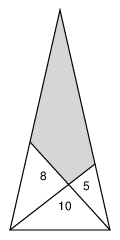
Solution by Chums
We decorate the diagram as shown:
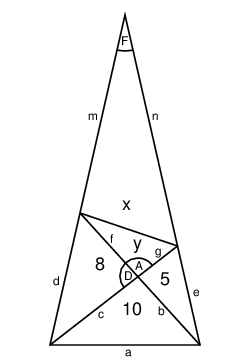
Let the desired area be \(U = x+y\).
Now, \(\sin A = \sin(\pi-D) = \sin D\). By the sine rule, \(\frac{1}{2}ab\sin A=10\) and \(\frac{1}{2}cf\sin D=\frac{1}{2}cf\sin A=8\).
As a result, \(8/cf = 10/cb\), so \(5f=4b\).
Similarly, \(\frac{1}{2}cb\sin D=10\) and \(\frac{1}{2}gb\sin D=5\) so \(2g=c\).
Also, \(\frac{1}{2}fg\sin A=y\) and \(\frac{1}{2}cb\sin A=10\), and that gives us \(\frac{y}{fg} = \frac{10}{cb}\), and so \(2ygb = ycb = 10fg\), and so \(yb = 5f = 4b\), and so \(y=4\). It remains to work out \(x\).
Now, \(x=\frac{1}{2}\sin F\), and the whole triangle has \[x+27 = \frac{1}{2}(m+d)(n+e)\sin F = x + \frac{1}{2}(me+dn+de)\sin F.\]
Hence \(\frac{1}{2}(me+dn+de)\sin F = 27\).
Also, by considering two other triangles we get \(\frac{1}{2}m(n+e)\sin F = x+9\) and \(\frac{1}{2}n(m+d)\sin F=x+12\). Subtracting our formula for \(x\) gives us \(\frac{1}{2}me\sin F=9\) and \(\frac{1}{2}nd\sin F=12\).
But as \(\frac{1}{2}me\sin F + \frac{1}{2}nd\sin F + \frac{1}{2}de\sin F=27\), we get \(\frac{1}{2}de\sin F = 6\).
This gives us that \(\frac{6}{de} = \frac{12}{nd}\), and so \(e = n/2\). This finally gives us that \(x = \frac{1}{2}mn\sin F = 2\frac{1}{2}me\sin F = 2\cdot 9=18\).
Hence \(U = x+y = 18+4 = 22\).