Question 1

Solution by Hobbit & Hercules

Preamble

Definition 1

We define \(T : \mathbb{N} \rightarrow \mathbb{R}\) by the formula \[T(n) = \sum_{k=0}^n \frac{1}{k!}.\]

Definition 2

As in the question, we define \(a_1 = 1\) and \(a_{n + 1} = (n + 1)(a_n + 1)\) for all \(n > 0\).

Definition 3

We define \(P : \mathbb{N} \rightarrow \mathbb{R}\) by the formula \[P(n) = \prod_{k=1}^n \left(1 +\frac{1}{ a_n}\right).\]

Proposition 1

\[P(n) = \frac{a_{n + 1}}{(n+1 )!}.\]

Proof

Let's consider a single factor of our product series, \(1 + \frac{1}{a_n}\). Note that \(1 + \frac{1}{a_n} = \frac{a_{n} + 1}{a_n}\). From Definition 2 we know that \(a_{n + 1} = (n + 1)(a_n + 1)\) which implies that \(a_n + 1 = \frac{a_{n+1}}{n+1}\). We can then substitute this into \(\frac{a_{n} + 1}{a_n}\) in order to obtain \(1 + \frac{1}{a_n} = \frac{a_{n+1}}{(n+1)a_n}\).

Now let's consider our product series using what we have learnt about each factor: \[P(n) = \left(1 + \frac{1}{a_1}\right)\left(1 + \frac{1}{a_2})(1 + \frac{1}{a_3})\cdots(1 + \frac{1}{a_n}\right).\] Applying our substitution for each factor we can write this in the form \[P(n) = \frac{a_2}{2 a_1} \frac{a_3}{3a_2} \cdots \frac{a_{n+1}}{(n+1)(a_n)}\] and by shifting each denominator to the left we get \[P(n) = \frac{1}{2a_1} \frac{a_2}{3a_2} \frac{a_3}{4a_3}\cdots\frac{a_n}{(n+1)(a_n)} a_{n+1}.\] At this point we can cancel out factors that appear in both the numerator and denominator to obtain \[P(n) = \frac{1}{1}\frac{1}{2}\frac{1}{3}\cdots\frac{1}{n}\frac{1}{(n+1)} a_{n+1} = \frac{a_{n+1}}{(n+1)!}.\]

We can now announce our solution:

Main solution

\[\prod_{k=1}^\infty \left(1 + \frac{1}{a_n}\right) = e.\]

Proof

Consider the functions \(P(n)\) and \(T(n)\). We will prove by induction on \(n\) that \(P(n) = T(n)\) for all \(n\). We will then deduce that both functions have the same limit as \(n \rightarrow \infty\), namely \(e\).

Proposition 2

\[P(n) = T(n).\]

Proof

This is a proof by induction on \(n\):

Base case:

We will show that \(P(1) = T(1)\). We have \(P(1) = (1 + \frac{1}{1}) = 2\) and \(T(1) = \frac{1}{0!} + \frac{1}{1!} = 1 + 1 = 2.\) Hence, \(P(1) =T(1) = 2.\)

Inductive step:

We will assume that \(P(n) = T(n)\). We want to show that \(P(n+1) = T(n+1)\). We know that \[P(n+1) = P(n)(1 + \frac{1}{a_{n+1}})\] and \[T(n+1)= T(n) + \frac{1}{(n+1)!}.\] But we know from Proposition 1 that \(P(n) = \frac{a_{n + 1}}{(n+1 )!}\). So \[P(n + 1) = \frac{a_{n + 1}}{(n+1 )!}(1 + \frac{1}{a_{n+1}}) = \frac{a_{n + 1}}{(n+1 )!} + \frac{1}{(n+1)!} = P(n) + \frac{1}{(n + 1)!}.\] But we assume that \(P(n) = T(n)\) which implies that \[P(n+1) = T(n) + \frac{1}{(n+1)!} = T(n+1),\] as required.

Therefore \(P(n) = T(n)\) for all positive natural numbers. This concludes Proposition 2.

Consequently, because \(P(n) = T(n)\) for all positive natural numbers \(n\) we conclude that they must have the same limit as \(n \rightarrow \infty.\) Therefore, since \[\lim_{n \to \infty} T(n) = e,\] we know that \[\lim_{n \to \infty} P(n) = \prod_{k=1}^\infty (1 + \frac{1}{a_n}) = e.\]

Remarks on Question 1

• This problem raises the interesting question "Can we write other Maclaurin and Taylor series as infinite products in this way?" For example, is it possible to write a number such as \(ln(2)\) in this way?
• Knowing that \[\lim_{n \to \infty} P(n) = \prod_{k=1}^\infty (1 + \frac{1}{a_n}) = e,\] we can now calculate \(e^x\). Indeed, we can think of it as \(\lim_{n \to \infty} \prod_{k=1}^n (1 + \frac{1}{a_n})^x = (e)^x = e^x.\)
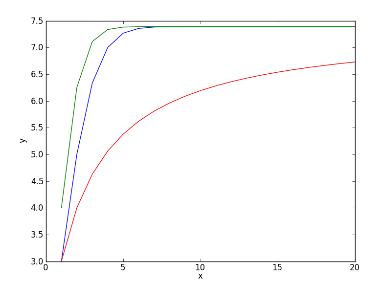
• Let \(P : (\mathbb{N},\mathbb{R}) \rightarrow \mathbb{R}\) be defined by taking \(P(n,x) =\prod_{k=1}^n (1 + \frac{1}{a_n})^x\). Let \(T : (\mathbb{N},\mathbb{R}) \rightarrow \mathbb{R}\) be defined by taking \(T(n,x) = \sum_{k=0}^n \frac{x^k}{ k!}\). Let \(G : (\mathbb{N},\mathbb{R}) \rightarrow \mathbb{R}\) be defined by taking \(G(n,x) = (1 + \frac{x}{n})^n\). By way of example, the graph below indicates what value of \(n\) is needed in order for \(P(n,2)\) (in green), \(T(n,2)\) (in blue), and \(G(n,2)\) (in red) to get close to their limiting value \(e^2\):
  
  We conjecture that for all \(x > 1\), we have \(P(n,x) > T(n,x) > G(n,x)\).